Introduction
Comme vous devez le savoir, je suis étudiant en sciences informatiques.
Comme vous le savez probablement également, mes deux grands dadas à ce niveau sont l'intelligence artificielle et la sécurité informatique.
Deux domaines qui peuvent paraitre assez éloignés mais qui d'après moi ne le sont pas tant que ça. Mais cela, j'y reviendrai.
Bref, dans l'un de mes cours, celui d'intelligence artificielle justement, nous voyons de beaux et puissants algorithmes pour les méthodes de recherches exhaustives.
Étant donné qu'ils sont excessivement intéressants et introduisent bien aux techniques et problématiques de l'intelligence artificielle, j'ai pensé vous en faire un petit cours en plusieurs posts.
Nous aurons ainsi 4 parties :
Tout un programme donc !
Et pour ne pas faire que parler en l'air, nous nous baserons sur un problème courant de l'intelligence artificielle, celui du cavalier sur l'échiquier.
Le problème du cavalier sur l'échiquier
Ce problème est un grand classique.
Même les plus grand maitre des échecs s'y sont collés.
Il consiste à faire parcourir à un cavalier toutes les cases d'un échiquier sans jamais repasser sur la même.
Le problème est d'autant plus amusant que la position du cavalier sur l'échiquier ne doit pas être fixée.
On doit pouvoir la choisir et la faire varier.
De plus, un autre paramètre est la taille de l'échiquier.
Nous voulons pouvoir essayer ce problème pour un échiquier de taille 6x7 si nous le souhaitons.
Un rappel pour les têtes en l'air
Pour les têtes en l'air, voici une explication sur les déplacements du cavalier :
– Contrairement aux autres pièces d’échecs, le Cavalier se déplace en sautant. Il n’est donc pas bloqué par ses propres pions comme peuvent l’être les Fous ou toutes les autres pièces du jeu d’échecs.
– Autre particularité, le Cavalier se déplace de 3 cases en dessinant un L majuscule. (2 cases horizontales + 1 verticale) ou (1 cases verticale + 2 horizontales).
Source : http://www.pousseurdebois.fr/cours/d...entducavalier/
Un immense espace de recherche
Si tous les joueurs d'échecs savent qu'un échiquier a un taille fixe de 8x8, c'est à dire 64 cases, il faut se rendre compte que ce nombre de cases crée un nombre titanesque de possibilités de coups.
Une borne supérieure de ce nombre de possibilités peut être calculée de la sorte :
On sait que pour chaque case de l'échiquier (64), le cavalier peut se rendre en maximum 8 cases.
Ces cases menant à leur tour à de nouveau choix.
Le nombre total de possibilités de mouvement est donc de : 64^8 = 281.474.976.710.656
Même pour un ordinateur, il n'est donc pas possible de les explorer toutes, nous allons donc devoir adopter une stratégie de résolution !
Une modélisation du problème
Avant de commencer à étudier une stratégie de résolution, nous allons devons modéliser notre problème c'est à dire le mettre dans une forme compréhensible par un ordinateur.
Pour ce faire, nous allons utiliser une modélisation par espaces d'états.
Celle-ci se compose de 4 éléments :
Voici un exemple :
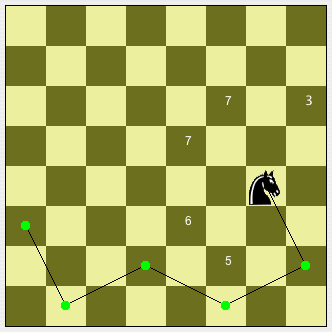
Si nous considérons cette situation comme la situation initiale notre état actuel est l'échiquier avec une seule case de prise, celle de départ.
Cet état est donc l'état de départ.
Imaginons qu'à chaque fois qu'une case est visitée, elle passe en couleur de fond bleue.
Un état final est alors le cavalier sur une autre case et toutes les autres cases avec une couleur de fond bleue.
L'ensemble des opérateurs est l'ensemble des coups possibles du cavalier dans cet état.
C'est à dire des coups qui ne le font pas sortir de l'échiquier et qui n'arrivent pas sur une case colorée en bleu.
Dans cette configuration, les coups possibles (opérateurs) sont affichés sur l'image
Cette modélisation nous permet de représenter le problème de manière logique et formelle.
C'est sur celle-ci que se basera notre future implémentation.
Les stratégies de résolution
Maintenant que nous avons une modélisation, nous pouvons approcher une stratégie de résolution.
Pour cette fois, nous n'en utiliserons qu'une, la stratégie en profondeur d'abord.
Derrière ce nom un peu barbare se cache en fait un système très simple.
Mais basons nous sur une image pour l'explication :

Cette image représente un graphe et les numéros sur chaque noeud est l'ordre dans lequel ceux ci sont développés
Nous avons donc ici un graphe et nous commençons au noeud numéroté 1 (comme c'est original n'est-ce pas ?).
Ce noeud a 3 fils numérotés. Ils représentent les états résultants de l'application des différents opérateurs applicables au noeud 1.
Comme vous le voyez, notre méthode de recherche en profondeur d'abord choisi de jouer le premier coup qu'elle trouve et de se rendre donc directement au noeud numéro 2 (nommé de la sorte qu'il est le second à être visité) et ce sans même vérifier si les noeuds 7 et 8, également accessibles ne sont pas des solutions directes au problème .
Une fois arrivé au noeud numéro 2, l'algorithme vérifie que ce noeud n'est pas une solution au problème. Ce qui n'est pas le cas.
Il évalue donc les différents opérateurs possibles et se rend compte qu'il y en a 2. Encore une fois, il choisi le premier coup possible et n'évalue pas directement les états résultants des autres coups.
L'algorithme arrive alors au noeud 3 et continue avec la même stratégie jusqu'à arriver au noeud numéroté 4.
Arrivé à ce dernier, il se rend compte que ce noeud n'est pas résultat mais qu'en plus, aucun opérateur n'est applicable. Il ne peut donc pas continuer sa recherche !
De ce fait, il remonte au noeud 3, le dernier visité et recommence a évaluer les opérateurs possibles.
Comme le choix du premier n'a rien donné. Il tente le second et arrive en 5.
Comme le 4 ce noeud n'a rien à offrir.
Retour en 3 donc mais sans plus de possibilités à visiter, notre algorithme remonte donc encore pour retourner au noeud numéro 2 et ré-évaluer ses opérateurs. Il choisit le second (le premier n'ayant rien donné) et arrive en 6.
Cet algorithme continue donc jusqu'à arriver, après de longue péripéties au noeud 12 qui est solution de notre problème.
Remarquez que le noeud 1 pourrait posséder d'autres fils que notre algorithme n'aura donc pas eu besoin de vérifier afin de trouver une solution intéressante ! C'est assez malin ça non ?
L'implémentation
Voici une implémentation en python de ce problème avec cette méthode de résolution.
Dans cette implémentation, l'état est défini par board, le plateau de jeu et par coordinates, les coordonnées actuelles du cavalier.
Le plateau est une matrice d'entier dont toutes les valeurs sont initialisées à 0.
Ainsi, lorsqu'une case est visité, cette valeur est passée à i (le numéro du coup) et on sait que cette case n'est plus valide.
Les opérateurs possibles sont donnés par la fonction moves qui se charge de vérifier à l'aide de la taille de l'échiquier et de la position quels sont les coups possibles.
La fonction finished permet de repérer si un état du plateau est un état final
Les fonctions cloneBoard et cloneResult sont des fonctions utilitaires permettant de copier le plateau et la solution avant de les envoyer dans les niveaux récursifs.
Cela permet de revenir à un état précédent en cas d'échec d'une branche de l'arbre.
Les fonctions cavalier et cavalier_term permettent respectivement de lancer et de gérer la récursion et la recherche de solutions.
Pour exécuter ce code, changez donc les variables globales width et height ainsi que l'appel à cavalier (0,0) impliquant que la case de départ est celle tout au dessus à gauche de l'échiquier.
Voici un exemple de résultat pour une plateau de 6x6 et un début en 0,0 :
La première liste représente les coordonnées successives de notre cavalier lors de ses déplacements.
La suite représente l'échiquier avec les cases numérotées dans l'ordre de passage.
Comme vous le voyez, l'implémentation vous propose de continuer la recherche pour trouver, le cas échéant, une autre solution.
Ce système simule en fait un échec dans la recherche de solution. Cela implique que l'algorithme continue sa recherche.
Voici un exemple :
Remarque sur l'implémentation
Ce code est fait en python 2 et est très largement perfectible.
Mon but n'était pas de faire un code syntaxiquement parfait mais bien de présenter le principe de résolution de ce problème.
Voici quelques pistes d'améliorations :
Remarquez qu'il a été prouvé que dans ce type de méthode de recherches, une implémentation multi-thread ne donne pas un gain significatif en efficacité.
En effet, les états sont trop inter-dépendants. La gestion de la concurrence des threads ferait donc perdre tout le gain de performance de leur utilisation.
Conclusion
Pour conclure, je vais vous proposer de lancer ce code pour un plateau de 8x8 (un vrai échiquier).
Lancez le puis aller prendre un café. Je peux vous assurer que lorsque vous reviendrez, il n'aura pas encore trouvé de solution.
C'est le problème de ce genre de techniques n'utilisant pas de connaissances propres au problème.
Elles font une merveilleuse recherche mais une recherche stupide dans le sens où elles ne regardent pas, dans notre cas, l'avantage de jouer un coup plutôt qu'un autre.
Par exemple, est-ce vraiment une bonne idée de tenter un coup après lequel notre cavalier sera "enfermé" ? Non évidement !
Un autre problème de cette technique, c'est qu'elle pourrait ne jamais se terminer.
Ce n'est pas le cas dans notre problème mais, si notre espace d'état est infini, l'algorithme pourrait partir sur une branche de résolution également infinie mais ne contenant aucune solution viable.
Dans le prochain article, nous repartirons donc de ce problème et nous approcherons la stratégie de recherche en largeur d'abord.
Plus tard nous continuerons encore en ajoutant des heuristiques de résolution à notre problème !
Si vous avez des questions, n'hésitez également pas à me les poser.
Je sais que cette matière n'est pas toujours facile à appréhender mais je suis là pour vous aider.
Une question de réflexion
Pouvez-vous me dire pourquoi, si vous demandez une nouvelle solution, elle arrive parfois très rapidement alors qu'à d'autres moments elle tarde à venir ?
Si vous pensez avoir la solution répondez moi postez le ici et envoyez moi la en privé.
Edit
Merci à Fred qui m'a bien aidé à faire une révision syntaxique du code afin de le rendre plus compréhensible
Comme vous devez le savoir, je suis étudiant en sciences informatiques.
Comme vous le savez probablement également, mes deux grands dadas à ce niveau sont l'intelligence artificielle et la sécurité informatique.
Deux domaines qui peuvent paraitre assez éloignés mais qui d'après moi ne le sont pas tant que ça. Mais cela, j'y reviendrai.
Bref, dans l'un de mes cours, celui d'intelligence artificielle justement, nous voyons de beaux et puissants algorithmes pour les méthodes de recherches exhaustives.
Étant donné qu'ils sont excessivement intéressants et introduisent bien aux techniques et problématiques de l'intelligence artificielle, j'ai pensé vous en faire un petit cours en plusieurs posts.
Nous aurons ainsi 4 parties :
- Une introduction à la méthode de résolution par espace d'état + une implémentation de recherche en profondeur d'abord
- Une implémentation en largeur d'abord
- Une implémentation en profondeur limitée d'abord
- Une implémentation ajoutant des heuristiques de résolutions
Tout un programme donc !
Et pour ne pas faire que parler en l'air, nous nous baserons sur un problème courant de l'intelligence artificielle, celui du cavalier sur l'échiquier.
Le problème du cavalier sur l'échiquier
Ce problème est un grand classique.
Même les plus grand maitre des échecs s'y sont collés.
Il consiste à faire parcourir à un cavalier toutes les cases d'un échiquier sans jamais repasser sur la même.
Le problème est d'autant plus amusant que la position du cavalier sur l'échiquier ne doit pas être fixée.
On doit pouvoir la choisir et la faire varier.
De plus, un autre paramètre est la taille de l'échiquier.
Nous voulons pouvoir essayer ce problème pour un échiquier de taille 6x7 si nous le souhaitons.
Un rappel pour les têtes en l'air
Pour les têtes en l'air, voici une explication sur les déplacements du cavalier :
– Contrairement aux autres pièces d’échecs, le Cavalier se déplace en sautant. Il n’est donc pas bloqué par ses propres pions comme peuvent l’être les Fous ou toutes les autres pièces du jeu d’échecs.
– Autre particularité, le Cavalier se déplace de 3 cases en dessinant un L majuscule. (2 cases horizontales + 1 verticale) ou (1 cases verticale + 2 horizontales).
Source : http://www.pousseurdebois.fr/cours/d...entducavalier/
Un immense espace de recherche
Si tous les joueurs d'échecs savent qu'un échiquier a un taille fixe de 8x8, c'est à dire 64 cases, il faut se rendre compte que ce nombre de cases crée un nombre titanesque de possibilités de coups.
Une borne supérieure de ce nombre de possibilités peut être calculée de la sorte :
On sait que pour chaque case de l'échiquier (64), le cavalier peut se rendre en maximum 8 cases.
Ces cases menant à leur tour à de nouveau choix.
Le nombre total de possibilités de mouvement est donc de : 64^8 = 281.474.976.710.656
Même pour un ordinateur, il n'est donc pas possible de les explorer toutes, nous allons donc devoir adopter une stratégie de résolution !
Une modélisation du problème
Avant de commencer à étudier une stratégie de résolution, nous allons devons modéliser notre problème c'est à dire le mettre dans une forme compréhensible par un ordinateur.
Pour ce faire, nous allons utiliser une modélisation par espaces d'états.
Celle-ci se compose de 4 éléments :
- Nos états : c'est un peu un photo du problème à un moment donné de sa résolution. Dans notre cas, c'est le cavalier sur une case de l'échiquier. Cet état contenant également l'ensemble des cases qui ont déjà été visitées
- Notre état initial : Dans notre cas, c'est le cavalier sur sa case de départ d'un échiquier de taille fixée. Aucune case n'a encore été visitée
- Notre ensemble d'états finaux : Ici ce sera toutes les possibilités de cases d'arrivée pour notre cavalier qui aurait parcouru toutes les autres cases
- Nos opérateurs : Ce sont les opérations que l'on peut utiliser pour passer d'un état à un autre. Dans notre cas, c'est l'ensemble des mouvements possibles du cavalier à partir d'une case donnée.
Voici un exemple :

Si nous considérons cette situation comme la situation initiale notre état actuel est l'échiquier avec une seule case de prise, celle de départ.
Cet état est donc l'état de départ.
Imaginons qu'à chaque fois qu'une case est visitée, elle passe en couleur de fond bleue.
Un état final est alors le cavalier sur une autre case et toutes les autres cases avec une couleur de fond bleue.
L'ensemble des opérateurs est l'ensemble des coups possibles du cavalier dans cet état.
C'est à dire des coups qui ne le font pas sortir de l'échiquier et qui n'arrivent pas sur une case colorée en bleu.
Dans cette configuration, les coups possibles (opérateurs) sont affichés sur l'image
Cette modélisation nous permet de représenter le problème de manière logique et formelle.
C'est sur celle-ci que se basera notre future implémentation.
Les stratégies de résolution
Maintenant que nous avons une modélisation, nous pouvons approcher une stratégie de résolution.
Pour cette fois, nous n'en utiliserons qu'une, la stratégie en profondeur d'abord.
Derrière ce nom un peu barbare se cache en fait un système très simple.
Mais basons nous sur une image pour l'explication :

Cette image représente un graphe et les numéros sur chaque noeud est l'ordre dans lequel ceux ci sont développés
Nous avons donc ici un graphe et nous commençons au noeud numéroté 1 (comme c'est original n'est-ce pas ?).
Ce noeud a 3 fils numérotés. Ils représentent les états résultants de l'application des différents opérateurs applicables au noeud 1.
Comme vous le voyez, notre méthode de recherche en profondeur d'abord choisi de jouer le premier coup qu'elle trouve et de se rendre donc directement au noeud numéro 2 (nommé de la sorte qu'il est le second à être visité) et ce sans même vérifier si les noeuds 7 et 8, également accessibles ne sont pas des solutions directes au problème .
Une fois arrivé au noeud numéro 2, l'algorithme vérifie que ce noeud n'est pas une solution au problème. Ce qui n'est pas le cas.
Il évalue donc les différents opérateurs possibles et se rend compte qu'il y en a 2. Encore une fois, il choisi le premier coup possible et n'évalue pas directement les états résultants des autres coups.
L'algorithme arrive alors au noeud 3 et continue avec la même stratégie jusqu'à arriver au noeud numéroté 4.
Arrivé à ce dernier, il se rend compte que ce noeud n'est pas résultat mais qu'en plus, aucun opérateur n'est applicable. Il ne peut donc pas continuer sa recherche !
De ce fait, il remonte au noeud 3, le dernier visité et recommence a évaluer les opérateurs possibles.
Comme le choix du premier n'a rien donné. Il tente le second et arrive en 5.
Comme le 4 ce noeud n'a rien à offrir.
Retour en 3 donc mais sans plus de possibilités à visiter, notre algorithme remonte donc encore pour retourner au noeud numéro 2 et ré-évaluer ses opérateurs. Il choisit le second (le premier n'ayant rien donné) et arrive en 6.
Cet algorithme continue donc jusqu'à arriver, après de longue péripéties au noeud 12 qui est solution de notre problème.
Remarquez que le noeud 1 pourrait posséder d'autres fils que notre algorithme n'aura donc pas eu besoin de vérifier afin de trouver une solution intéressante ! C'est assez malin ça non ?
L'implémentation
Voici une implémentation en python de ce problème avec cette méthode de résolution.
Dans cette implémentation, l'état est défini par board, le plateau de jeu et par coordinates, les coordonnées actuelles du cavalier.
Le plateau est une matrice d'entier dont toutes les valeurs sont initialisées à 0.
Ainsi, lorsqu'une case est visité, cette valeur est passée à i (le numéro du coup) et on sait que cette case n'est plus valide.
Les opérateurs possibles sont donnés par la fonction moves qui se charge de vérifier à l'aide de la taille de l'échiquier et de la position quels sont les coups possibles.
La fonction finished permet de repérer si un état du plateau est un état final
Les fonctions cloneBoard et cloneResult sont des fonctions utilitaires permettant de copier le plateau et la solution avant de les envoyer dans les niveaux récursifs.
Cela permet de revenir à un état précédent en cas d'échec d'une branche de l'arbre.
Les fonctions cavalier et cavalier_term permettent respectivement de lancer et de gérer la récursion et la recherche de solutions.
Code:
# -*- coding: UTF-8 -*-
import sys
WIDTH = 6
HEIGHT = 6
CASE_NON_VISITEE = '0'
def cloneResult(coordinates):
"""Copie des solutions précédentes"""
copy = list()
for (a,b) in coordinates:
copy.append((a,b))
return(copy)
def cloneBoard(board):
"""clone de l'échiquier"""
cpy = list()
for line in board:
lcopy = list()
cpy.append(lcopy)
for column in line:
lcopy.append(column)
return cpy
def get_moves(a, b):
"""Vérifie à partir de la coordonnée du cavalier si les déplacements
sont possibles et ne sortent pas de l'échiquier"""
# (1, 2) déplacement d'une case à droite et deux cases vers le bas
deplacements = [(1,2),(-1,2),(1,-2),(-1,-2),
(2,1),(-2,1),(2,-1),(-2,-1)]
moves = [] # Enregistrement des coordonnées possibles où le cavalier peut aller
for w, h in deplacements:
x = a + w
y = b + h
if(x >= 0 and x < WIDTH and y >= 0 and y < HEIGHT):
moves.append((x, y))
return(moves)
def put(startW, startH):
"""placement de la figure à une coordonnée de départ et lance la résolution"""
# que du vide sur l'échiquier pour l'instant
board = [[CASE_NON_VISITEE for x in range(WIDTH)] for y in range(HEIGHT)]
board[startW][startH] = 1 # Car la case de départ est la première visitée
number = 2 # Numéro d'ordre de la prochaine case visitée
result = [(startW, startH)]
cavalier_term(startW, startH, board, result, number)
def is_finished(board):
"""Vérifie si toutes les cases ont été visitées (c'est à dire si elles ont toutes un numéro d'ordre)"""
for line in board:
for case in line:
if(case == CASE_NON_VISITEE):
return False
return True
def printBoard(board):
"""Affichage de l'échiquier"""
print("Board : ")
for line in board:
line = map(str, line) # On transforme les entiers de la ligne en chaîne pour les écrire
line = '[' + '\t'.join(line) + ']' # ligne de la forme [0 0 0 0 0 0]
print(line)
def cavalier_term(w, h, board, result, number):
""" Cette fonction est la fonction récursive permettant la résolution à proprement parler"""
if is_finished(board): # On vérifie si on est dans un état final (çad où toutes les cases ont été visitées)
print(result)
printBoard(board)
if raw_input("Continue (T-F) ? ") != "T":
sys.exit(0)
else:
for w, h in get_moves(w, h): # On récupère les mouvements possibles dans la situation actuelle
if int(board[w][h]) < 1: # On s'empêche de revisiter une case déja visitée
b = cloneBoard(board)
b[w][h] = number # On marque la case actuelle comme visitée
r = cloneResult(result) # On clone les résultats afin de pouvoir les récupérer en cas d'échec du ou des mouvements suivants
r.append((w,h)) # On ajoute le coup que l'on s'apprête à jouer dans la liste des résultats
n = number+1 # On incrémente le numéro d'ordre des cases
cavalier_term(w, h, b, r, n) # On fait l'appel récursif pour relancer la résolution dans le nouvel état
put(0, 0)
Voici un exemple de résultat pour une plateau de 6x6 et un début en 0,0 :
Code:
[(0, 0), (1, 2), (2, 4), (3, 2), (4, 4), (5, 2), (4, 0), (2, 1), (4, 2), (5, 0), (3, 1), (1, 0), (0, 2), (1, 4), (3, 5), (5, 4), (3, 3), (4, 5), (5, 3), (4, 1), (2, 0), (0, 1), (2, 2), (3, 4), (5, 5), (4, 3), (5, 1), (3, 0), (1, 1), (0, 3), (1, 5), (2, 3), (0, 4), (2, 5), (1, 3), (0, 5)] Board : [1 22 13 30 33 36 ] [12 29 2 35 14 31 ] [21 8 23 32 3 34 ] [28 11 4 17 24 15 ] [7 20 9 26 5 18 ] [10 27 6 19 16 25 ] Continue (T-F) ?
La suite représente l'échiquier avec les cases numérotées dans l'ordre de passage.
Comme vous le voyez, l'implémentation vous propose de continuer la recherche pour trouver, le cas échéant, une autre solution.
Ce système simule en fait un échec dans la recherche de solution. Cela implique que l'algorithme continue sa recherche.
Voici un exemple :
Code:
[(0, 0), (1, 2), (2, 4), (3, 2), (4, 4), (5, 2), (4, 0), (2, 1), (4, 2), (5, 0), (3, 1), (1, 0), (0, 2), (1, 4), (3, 5), (5, 4), (3, 3), (4, 5), (5, 3), (4, 1), (2, 0), (0, 1), (2, 2), (3, 4), (5, 5), (4, 3), (5, 1), (3, 0), (1, 1), (0, 3), (1, 5), (2, 3), (0, 4), (2, 5), (1, 3), (0, 5)] Board : [1 22 13 30 33 36 ] [12 29 2 35 14 31 ] [21 8 23 32 3 34 ] [28 11 4 17 24 15 ] [7 20 9 26 5 18 ] [10 27 6 19 16 25 ] Continue (T-F) ? T [(0, 0), (1, 2), (2, 4), (3, 2), (4, 4), (5, 2), (4, 0), (2, 1), (4, 2), (5, 0), (3, 1), (1, 0), (0, 2), (1, 4), (3, 5), (5, 4), (3, 3), (4, 5), (5, 3), (4, 1), (2, 0), (0, 1), (2, 2), (3, 0), (5, 1), (4, 3), (5, 5), (3, 4), (1, 5), (0, 3), (1, 1), (2, 3), (0, 4), (2, 5), (1, 3), (0, 5)] Board : [1 22 13 30 33 36 ] [12 31 2 35 14 29 ] [21 8 23 32 3 34 ] [24 11 4 17 28 15 ] [7 20 9 26 5 18 ] [10 25 6 19 16 27 ] Continue (T-F) ? T [(0, 0), (1, 2), (2, 4), (3, 2), (4, 4), (5, 2), (4, 0), (2, 1), (4, 2), (5, 0), (3, 1), (1, 0), (0, 2), (1, 4), (3, 5), (5, 4), (3, 3), (4, 5), (5, 3), (4, 1), (2, 0), (0, 1), (2, 2), (0, 3), (1, 5), (3, 4), (5, 5), (4, 3), (5, 1), (3, 0), (1, 1), (2, 3), (0, 4), (2, 5), (1, 3), (0, 5)] Board : [1 22 13 24 33 36 ] [12 31 2 35 14 25 ] [21 8 23 32 3 34 ] [30 11 4 17 26 15 ] [7 20 9 28 5 18 ] [10 29 6 19 16 27 ] Continue (T-F) ?
Ce code est fait en python 2 et est très largement perfectible.
Mon but n'était pas de faire un code syntaxiquement parfait mais bien de présenter le principe de résolution de ce problème.
Voici quelques pistes d'améliorations :
- Entrée interactive ou via la ligne de commande des paramètres
- Optimisation des fonctions de copie des données
- ...
Remarquez qu'il a été prouvé que dans ce type de méthode de recherches, une implémentation multi-thread ne donne pas un gain significatif en efficacité.
En effet, les états sont trop inter-dépendants. La gestion de la concurrence des threads ferait donc perdre tout le gain de performance de leur utilisation.
Conclusion
Pour conclure, je vais vous proposer de lancer ce code pour un plateau de 8x8 (un vrai échiquier).
Lancez le puis aller prendre un café. Je peux vous assurer que lorsque vous reviendrez, il n'aura pas encore trouvé de solution.
C'est le problème de ce genre de techniques n'utilisant pas de connaissances propres au problème.
Elles font une merveilleuse recherche mais une recherche stupide dans le sens où elles ne regardent pas, dans notre cas, l'avantage de jouer un coup plutôt qu'un autre.
Par exemple, est-ce vraiment une bonne idée de tenter un coup après lequel notre cavalier sera "enfermé" ? Non évidement !
Un autre problème de cette technique, c'est qu'elle pourrait ne jamais se terminer.
Ce n'est pas le cas dans notre problème mais, si notre espace d'état est infini, l'algorithme pourrait partir sur une branche de résolution également infinie mais ne contenant aucune solution viable.
Dans le prochain article, nous repartirons donc de ce problème et nous approcherons la stratégie de recherche en largeur d'abord.
Plus tard nous continuerons encore en ajoutant des heuristiques de résolution à notre problème !
Si vous avez des questions, n'hésitez également pas à me les poser.
Je sais que cette matière n'est pas toujours facile à appréhender mais je suis là pour vous aider.
Une question de réflexion
Pouvez-vous me dire pourquoi, si vous demandez une nouvelle solution, elle arrive parfois très rapidement alors qu'à d'autres moments elle tarde à venir ?
Si vous pensez avoir la solution répondez moi postez le ici et envoyez moi la en privé.
Edit
Merci à Fred qui m'a bien aidé à faire une révision syntaxique du code afin de le rendre plus compréhensible



 .
.
Commentaire